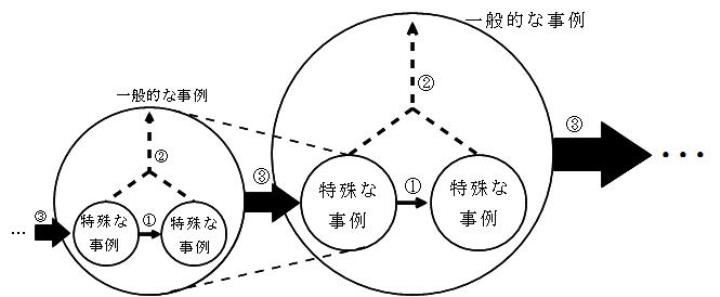
算数・数学の授業では，子どもたちは一所懸命に考えています。ということは，その考え方を明らかにすることができるなら，授業をどのように観ればよいか，どのように創ればよいか，ということにもつながるはずです。考え方を捉える視点は様々ありますが，推論（ある前提から結論を導く思考）に着目すると，演繹（※１），帰納（※２），類推（※３）の3つで捉えることができます。演繹は論理的な考え方であり，帰納と類推は発見的な考え方です。
　算数・数学の特徴には「一般性」や「抽象性」などがありますが，他教科にはない特徴として，「系統性」を指摘できます。つまり，既に知っていることを発見的な考え方によって拡張して新しいことを知ることができる，という特徴が算数・数学の授業にはあります。
　このような特徴に基づけば，子どもたちがどのような「既に知っていること」を使って知ろうとしているのか，という点で算数・数学の授業を観ることが重要です。そして，そのような子どもたちのデータに基づけば，「Aということを知るために，この子どもたちの学習経験からBということを使うだろう」と予測して授業を創ることができます。

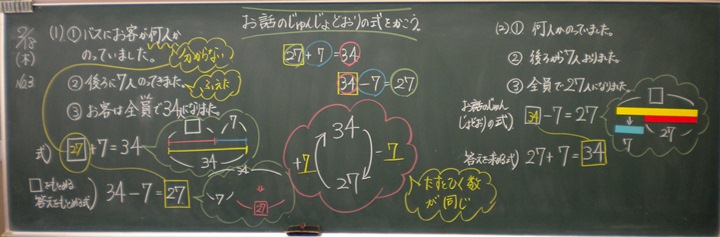
　小学校「算数」と中学・高等学校「数学」には，教科名だけでなく内容にも違いがあります。端的には，「文字」と「証明」が導入されることで数学の見方が変わるため，それらの間にはギャップが生じます。例えば，文字に着目してみましょう。
　小学校算数では，整数・小数・分数の四則演算について学習します。そのため，式は計算結果を導くためのものになります。そして，文字が導入されると，それまで「1＋2」や「0.1＋0.2」「1/2＋1/3」と表されていたものが，すべて「a＋b」と表されることになります。そうすると，様々な数を文字に置き換えたことになるので，計算結果ではなく「a＋b」が何を意味しているのか，たし算にはどのような性質があるのか，などのように見方が変わっていきます。そこにギャップがあるのです。
　そのようなギャップを埋めるため，小学校算数の段階で代数的推論（※４）を伸ばすことができれば，中学校の文字式の学習につながります。そこで，算数の授業をそのように観ると，低学年のころから代数的推論が現れることがわかり，それを伸ばすための授業を創ることも可能になるのです。