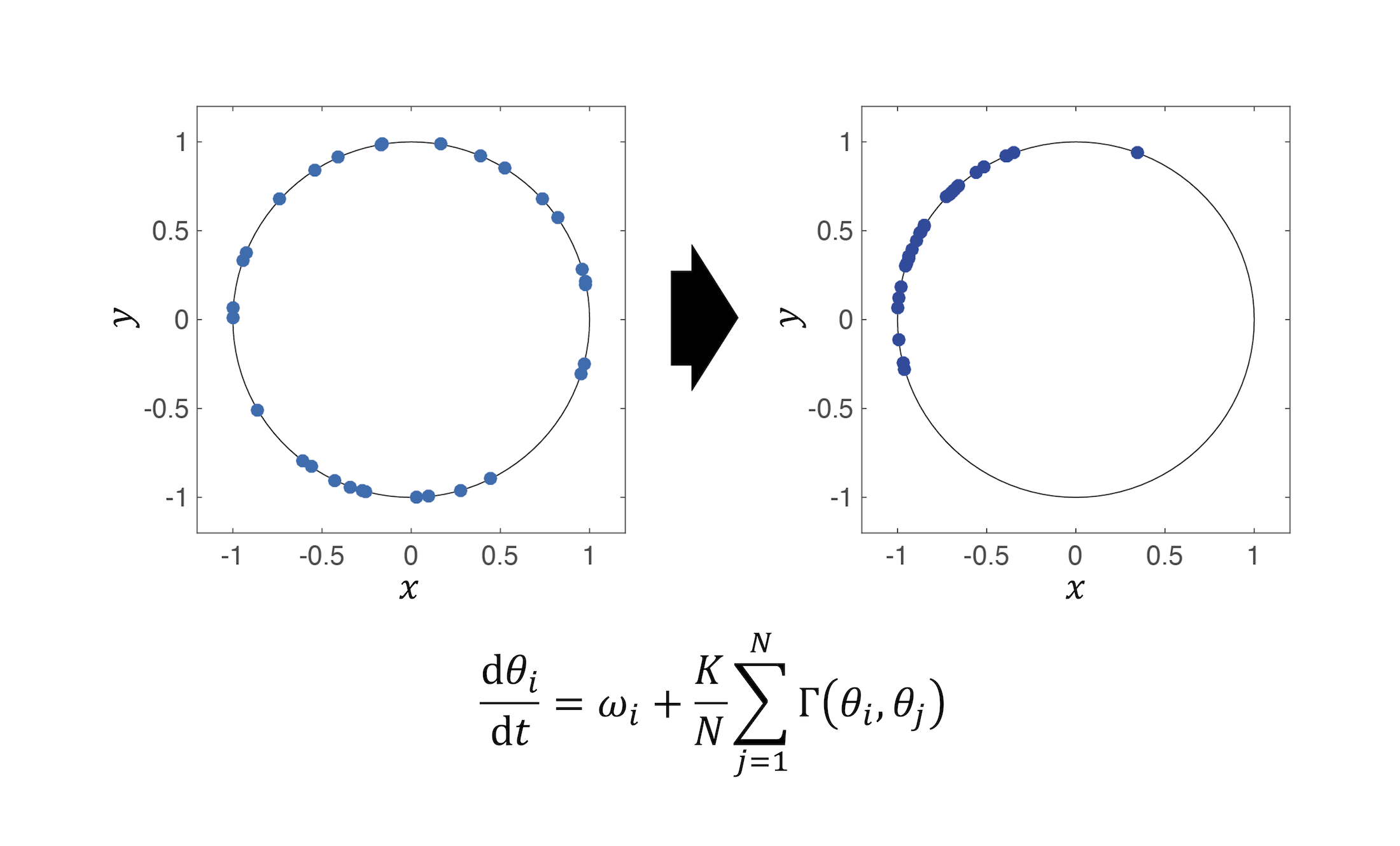
私たちの身の回りには自律的なリズムを持つ物質・システムが存在します。脈動する心筋細胞、電気パルスを発する神経細胞、発光するホタル、生物の体内時計、生態系における動物数の時間推移など、リズムは様々な場所に多様なスケールで存在します。さて、このような自律リズムを持つ素子が複数集まると集団のリズムが揃うことが知られています。「同期現象」と呼ばれるこの現象は、心臓を構成する心筋細胞の集団脈動、ホタルの集団発光、遠隔地の気象や植物の種子生産量の同調など、私たちの身の回りで広く観測されます。また近年では、発電所から街まで電気を送る電力ネットワークの効率化、病理の治療といった応用技術にリズムの同期が有用となる可能性が示されており、これらの実現のために同期現象の理解が求められています。この枠組みにおいて私は、同期が起こるメカニズム、リズムの同期が実世界にもたらす影響に興味を持って研究をしています。リズム素子の挙動を記述する方程式の理論解析やコンピュータシミュレーションを通して、同期現象の理解を進めています。

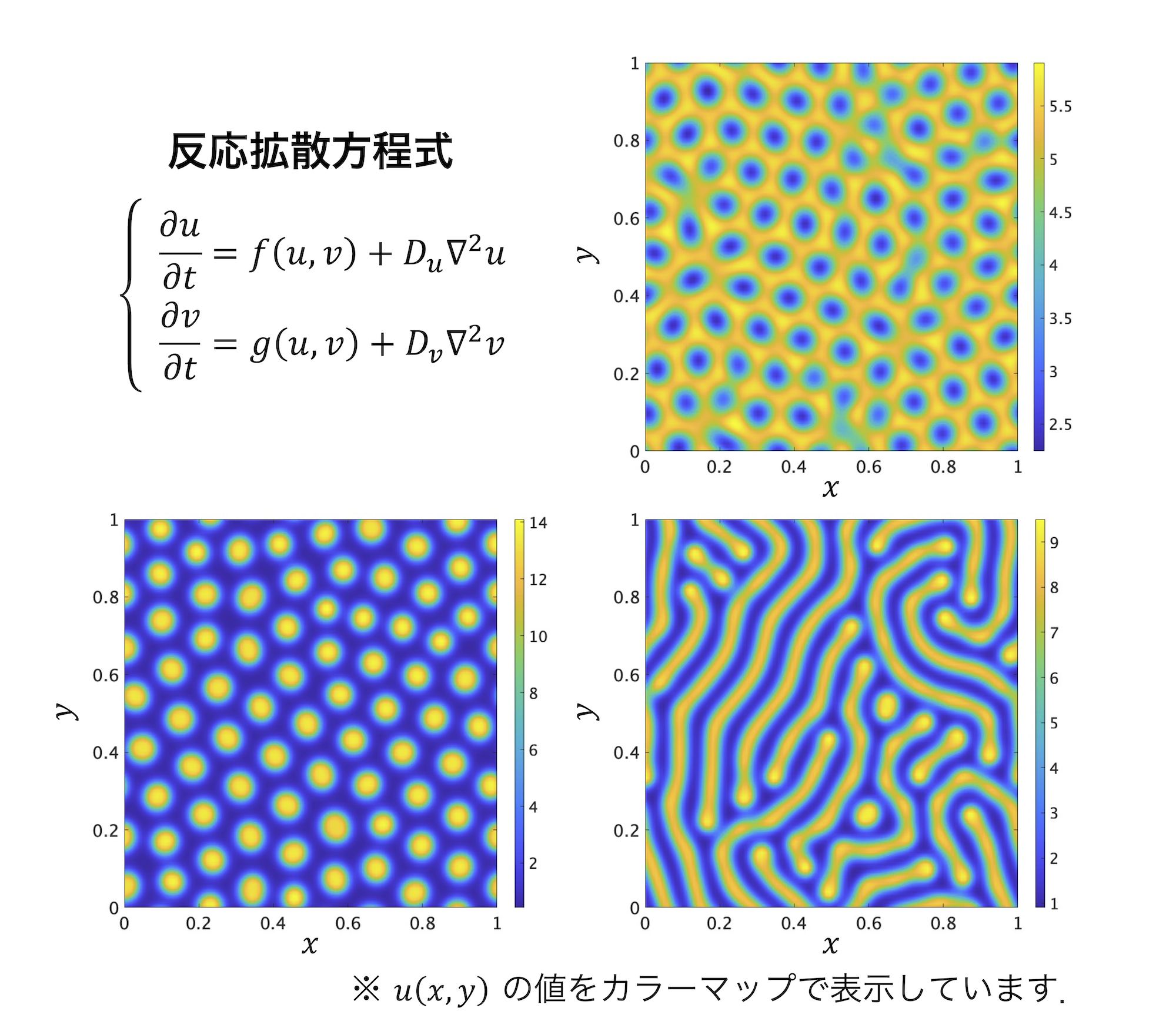
動物の表皮の模様、植物の形、鉱石に見られる模様など、私たちの身の回りには、まるでデザインされたかのように美しい形・模様があります。しかしながら自然界にデザイナーはいません。上で挙げた形や模様は全て物理現象の結果として自律的に（つまり"勝手に"）形成されます。「パターン形成」と呼ばれるこの現象は、私たちの身の回りに普遍的に存在する一方で、その多くは原理が解明されていません。私は、このパターン形成を研究の対象として、自然界において自律的に形が形成される原理を理論的に調べています。特に、反応物質が媒質内を拡散することで形成されるパターンに興味を持っていて、これを記述する「反応拡散方程式」の理論解析やコンピュータシミュレーションを通してパターン形成の原理を探っています。また、この方程式は生態系における生物数の時間変化を部分的に記述し得ることが知られています（捕食被食が反応に、生息域における生物種の移動が拡散に対応します）。この点に着目し、同方程式の解析が生態系に対する新たな理解につながる可能性を模索しています。