素朴な数え上げの背後に
数学の中でも、物の数を数えるというのは基本的な問題です。例えば、 10個のものから2個を選ぶ組合せは45通りですし、n個のものから2個を選ぶ組合せは n(n-1)/2 通りあります。これらは簡単ですが、次に自然数nを足し算で表す方法は何通りあるか考えてみましょう。ただし、数を足す順番は無視します。例えば5は、 5=4+1=3+2=3+1+1=2+2+1=2+1+1+1=1+1+1+1+1 の7通りあります。ここで""5""自身も数えています。さて、このように自然数nを足し算で分解する場合の数を、nの分割数といいます。上の例のように、5の分割数は7になります。では一般にnの分割数は、nを使って表せるでしょうか。
意外に思うかもしれませんが、nの分割数を n(n-1)/2 のように簡単に表す表示式は無いのです。具体的な式で書けないため、分割数を考えるときは色々と工夫をする必要があります。このように簡単な数え上げの問題でも、簡単な答えが用意されているとは限りません。一見小学生レベルの問題のようですが、研究ではもっと高度な数学が必要になるのです。
数え上げからいろいろな数学へ
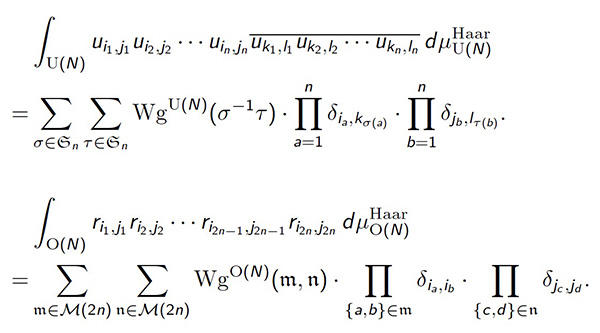
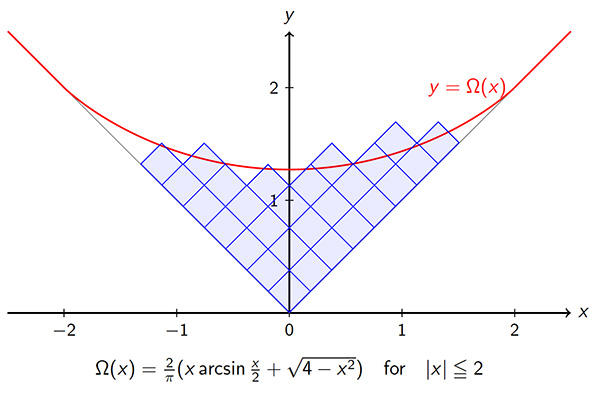
自然数nの分割に、図のように箱を並べたものを対応させます。これはヤング図形と呼ばれるもので、数学の様々な分野に登場します。私の研究では、このヤング図形がランダムに与えられたときの現象の解明に取り組んでいます。ヤング図形がある具体的な確率のもとで生成され、そしてそのヤング図形がとても大きいとき、確率論の言葉を使って現象を説明します。もう少し正確に言うと、n を無限大に近づけるときの極限定理を見つけます。例えば図のΩという関数は、とても大きなヤング図形のスケーリング極限形の一種を与えています。
素朴な概念であるヤング図形は様々な分野に登場します。例えば群の表現論(※1)が代表的です。私は表現論も研究していますが、ヤング図形が関連する別の分野、ランダム行列というものも研究しています。ランダム行列は、行列の成分が確率変数になっているものです。先ほどのヤング図形と一見関係がないように思えますが、実は大きなヤング図形と大きなランダム行列には不思議な類似点がたくさん発見されているのです。そのような類似点は他の対象物にも見られ、それらを明らかにしていくことを目指しています。
用語解説
*1:群とは対象の対称性を抽象化したもので、大学2,3年頃に学習します。表現論とは、群などの性質を線形代数(行列やベクトル)で説明する数学の分野です。