中学・高校では理科の授業が楽しくて，特に生物と物理が好きでした。これらの共通点は，雑談を交えたコミカルで面白い説明でした。実は，この物理の先生は隣に住んでいる同い年の親友のお父さんでした。
授業中の雑談で一度，大学時代の研究のエピソードを話してくれたことがあります。それは，微粒子の運動法則を調べるため，顕微鏡で飛び交う粒子を長時間観察するという実験でした。睡魔に襲われながら観察していると一瞬うたた寝をしてしまい，実験がやり直しになってしまったという話でした。当時，運動方程式しか知らない私には，どうやって微粒子の運動法則を記述するのか見当がつかず，途方もないテーマだと感じました。
その日家に帰ると，数学者の父が自分の研究がうまくいったと自慢してきました。その研究は，無限個の相互作用するブラウン運動粒子（＊１）に関する研究で，運動を記述する方程式が解けたという話でした。詳細は理解できませんでしたが，数学が厳密かつ抽象的であるというイメージが覆されました。実際には，空想的な無限個の粒子という対象を扱える柔らかさと，運動を具体的に記述する緻密さの両方を持っていると感じました。
これが，私が今研究している粒子系（＊２）との出会いです。

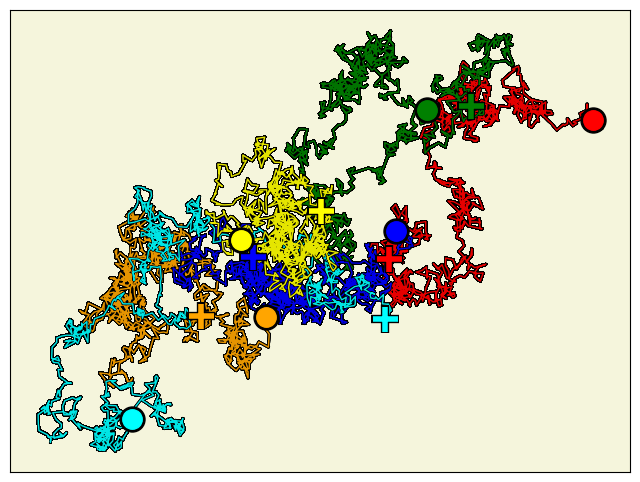
私は，粒子のランダム配置や運動について研究しています。ここで言う粒子は数学的な対象です。空間中に漂う微粒子などの物体だけでなく，買い物の選び方，デジタル写真，文章などの情報も粒子として扱うことができます。
ランダムな粒子配置は，点過程と呼ばれます。整数上の点過程（＊３）の簡単な例を２つ考えてみましょう。１つ目は，各整数に対してコインを投げて表が出たら粒子を配置し，裏が出たら粒子を配置しない，というルールで決まる粒子配置です。この粒子配置の分布はBernoulli（ベルヌーイ）点過程と呼ばれます。２つ目は，一回コインを投げて表が出たら偶数の場所に粒子を配置し，裏が出たら奇数の場所に配置する，というルールで決まる粒子配置です。これを格子点過程と呼ぶことにしましょう。前者の粒子配置は完全にデタラメで，粒子同士は無相関です。後者はランダムですが，１箇所分のランダムさしかないため，１つの粒子の場所が決まれば他の全ての粒子の場所も決まってしまいます。これらの間に中間的な点過程がたくさんあります（＊４）。私の興味の１つは，点過程がBernoulli点過程と格子点過程のどちらに近いのかを解明することです。目標は，点過程における粒子系の相互作用を記述することや，相互作用する粒子系の運動法則を明らかにすることです。